The physical concept behind the simulation is to calculate the position of all the stars at different equally spaced moments. When you do that you will see that the stars rotate around a common center.
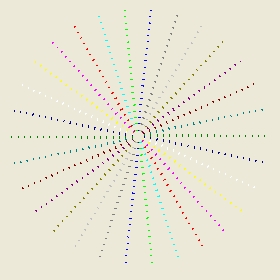
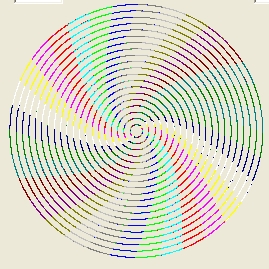
The two pictures below show the result such a simulations. Each simulation in both pictures involves 600 stars.
|
^ | | | |
|
^ | | | |
- The left picture shows the initial position of the stars and almost no historical positions.
- The right picture shows a much longer simulation and more historical positions. As such you can follow the positions of each star. Each path follows a circle and the galaxy is stable. (*)
In the simulation all the positions of the stars are calculated as a function of the previous positions of all the stars and when that is done the display is updated. That means when you observe the display at each update you get an instantaneous diplay of the present position of all the stars.
In reality this is not possible. Suppose you are hanging in a helicopter straight above the center (Black Hole) of the galaxy. The most current view at that position is the center of the galaxy. All the other stars you observe in the past. This delay is a function of distance and the speed of light.
The left picture shows (almost) the initial position of all the stars. The structure is like the spokes of a wheel in straight lines. In each simulation that means there are 30 spokes.
In reality when you are hovering above the center when you start the simulation what you see is first the star of the most inner ring. This is "star 1". Next the star in ring two. This is "star 2" etc etc and finally star 30. All these 30 stars become visible in a straight line. However when "star 30" becomes visible "star 1" is not any more at its initial position but has moved forward, counter clockwise.
The reason why this exercise is important is because when you consider to perform a simulation based on real situation i.e. actual stars. Suppose you are capable to measure instantaneous the position of all the stars. In that case, even if you can measure all the positions simultaneous, what you have measured are not the positions of all the stars at the same moment but at different moments in the past. This time difference in the past is a function of the distance and the speed of light. To calculate the positions at the same moment you need at least the speed of all the stars.
The same problem arises when you want to test at the end of the simulation the predicted results in the future with actual observations: again you have to take the time delays into account.
The important lesson is here that only when actual observations are involved, that means at the beginning to calculate the initial positions and at the end to test the results, the speed of light is important, not during the actual simulation i.e. calculation. The simulation is a mathematical model that describe the processes involved, in this case the movements of the stars in a galaxy. These processes are almost completely independent of the speed of light, photons neutrinos and single atomic particles.
(*) When you observe the simulations sooner or later chaos starts and all structures disappear. The reason does not lie in the physical realm, but is purely caused by computer limitations i.e. accuracy.
Spiral arms
In this simulation the total number of stars is 600. That is very small. In reality the Milky Way consists of 10^12 Solar masses and the radius is between 50000 and 90000 lightyears. This information comes from Wikipedia. Select this: Milky Way This same document also shows the GRC. Select this: Milky Way - GRC To observe the GRC from M33 select this:M33 GRCThe most important lesson to learn is that the two GRC's are rather different. This requires an explanation.
As mentions above the simulation only involves 600 stars. In fact each of these stars is a collection of thousands of stars. By combining the stars you make the simulation possible. In Picture B you see an image of a spiral arm. In reality when you perform a simulation with more stars you will not get spiral arms, but a structure which is only rotational symmetric like an elliptical galaxy. To observe spiral arms you have to inject huge "gas clouds" which will move radial towards the center of the galaxy.
Dark Matter
The issue of spiral arms also touches a different issue and that is the concept of dark matter. Dark matter is supposedly not the same as ordinary matter or baryonic matter but something different i.e. non-baryonic matter. Baryonic matter we also call visible matter. This naming convention is rather strange because all matter is inprinciple invisible. When you place yourself in a room and you turn off all the light you become not visible, still the matter human beings are made from (= baryonic matter) is called visible matter.This baryonic matter is only becoming visible when the internal processes involved are heated and the temperature increases. When this happens the radiation they emit change into the visible frequency range and become visible by the human eye. That means that baryonic matter depending about certain circumstances can be either observed or is not observed. As a consequence it is very difficult to measure directly (based on visibility) all the baryonic matter in a galaxy, because a huge amount can de invisible for the human eye.
A similar problem exists when you study the spiral arms in a spiral galaxy. Spiral arms are parts of a galaxy disc which contains more visible mass (stars) than in the space in between. That means it does not make sense to proclaim that there is more baryonic matter in this "in between" space than in the arms. The issue is how do you explain this apparent discrepancy, the fact that the supposed involved dark matter is not every where available in the same amounts. With explain meaning the processes involved i.e. galaxy evolution. A much more logical assumption is that throughout the disc there is baryonic dust in order to explain the missing matter issue.